El término logaritmo deriva del griego logos que significa razón y de arithmos que quiere decir números. En matemática, el logaritmo es el exponente que se necesita para elevar un número que es positivo y que resulte el número esperado.
El logaritmo del número x que tiene como base a es el número al que se eleva a para lograr los resultados del número x. La base que es a tiene que ser distinta al 1 pero mayor que el cero. Ejemplo: ay = x ⇒loga x = y . Esto quiere decir que el logaritmo de x cuya base es igual a la y, tiene que cumplir la condicionante de que esa base tenga un valor mayor que el cero y diferente a uno. Ejemplo: 22= 4 ⇒log 2 4=2.
Los caminos que condujeron al descubrimiento de los logaritmos por John Napier de Escocia y Jobst Burgi de Suiza, en el año 1615, fueron dos: Los cálculos de trigonometría para el estudio de las investigaciones astronómicas que eran aplicadas a la navegación y el cálculo de riquezas acumuladas sobre las reglas del interés compuesto.
Los logaritmos resuelven con mucha facilidad problemas de geometría y aritmética. El primero en realizar las tablas logarítmicas en base 10 fue Henry Briggs, en el año 1631.
¿CUALES SON SUS PARTES?
Partes del Logaritmo
Logaritmo
Es el exponente que tiene una potencia con una base, o el número al que se tiene que elevar esa base que ya ha sido dada para llegar al resultado.
Antilogaritmo
Es una función que es contraria a un logaritmo. También se denomina antilogaritmo N de un número m, con relación a la base a, en el número donde m es el logaritmo. Ejemplo: n = logb X
Base del logaritmo
La base de un logaritmo es siempre positiva y el número 1 no se puede tomar como la base de un logaritmo. La base que tiene un logaritmo es un número real y positivo, pero diferente al 1.
Mantisa
También se denomina significando. Es una parte de la representación que en un punto flotante tiene los dígitos necesarios y significativos del número que se representará.
La magnitud de la misma queda determinada por el exponente. Está constituida por un número que es real con una parte entera que tiene un dígito, que es el primer valor que representarán.
Característica
En la característica se señala la posición que tiene la coma decimal en un número que es asociado. La característica en algunos logaritmos se encuentra por la observación.
Argumento o antilogaritmo
El argumento de un logaritmo también está constituido por un número real que es positivo.
Exponente o exponencial de un logaritmo
Se denomina exponente o exponencial al número que es positivo y que se eleva a un tipo de variable x.
Potencia
La potencia es un número determinado, puede ser cualquiera, que recibe el nombre de base y se eleva a otro tipo de número que recibe el nombre de exponente y del cual se obtiene un resultado. Tanto la potencia como el logaritmo se pueden expresar como una potencia.
Cologaritmo
Se denomina cologaritmo del número N a un logaritmo del que es su reciproco.
Función logarítmica
También se denomina función de un logaritmo y es una aplicación que es biyectiva de los grupos de números reales que son positivos, pero sin el cero, en todo el conjunto de los números llamados reales.
Clases de logaritmo
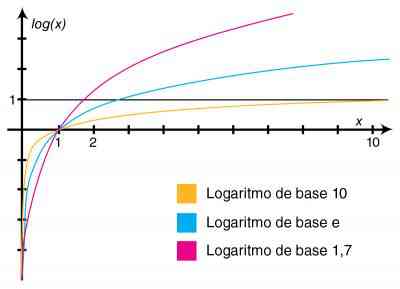
Logaritmo decimal
Es el que lleva como base un número 10.
Logaritmo neperiano o natural
Es un logaritmo cuya base es un número e.
Propiedades logarítmicas
- No hay algoritmo que tenga su base negativa.
- No hay logaritmo de números negativos.
- No hay logaritmos de un número cero.
- El logaritmo de 1 siempre es cero.
- Cuando el logaritmo es base a es porque a es igual a 1. Ejemplo: loga a =1.
- Un logaritmo que tiene como base a es igual que el exponente que tiene. Ejemplo: loga an = n
- El logaritmo que tiene un producto es el mismo que resulta de sumar los logaritmos que hay en los factores. Ejemplo: loga (X.Y) = loga X + loga Y.
